Decision trees are a highly useful visual assistance in analyzing a series of predicted outcomes for a particular model. As such, it is often used every bit a supplement (or fifty-fifty culling to) regression analysis in determining how a serial of explanatory variables will impact the dependent variable.

In this particular example, we analyse the impact of explanatory variables of age, gender, miles, debt, and income on the dependent variable car sales.

Classification Problems and Decision Trees

Firstly, we load our dataset and create a response variable (which is used for the classification tree since we demand to catechumen sales from a numerical to categorical variable):

We then create the training and test data (i.e. the information that nosotros will employ to create our model and so the data we volition examination this data confronting):

#Create training and test data inputData <- fullData[1:770, ] # training data testData <- fullData[771:963, ] # examination data

Then, our classification tree is created:

#Classification Tree library(rpart) formula=response~Age+Gender+Miles+Debt+Income dtree=rpart(formula,information=inputData,method="grade",control=rpart.control(minsplit=30,cp=0.001)) plot(dtree) text(dtree) summary(dtree) printcp(dtree) plotcp(dtree) printcp(dtree)

Note that the cp value is what indicates our desired tree size – nosotros see that our Ten-val relative error is minimized when our size of tree value is 4. Therefore, the determination tree is created using the dtree variable by taking into business relationship this variable.

summary(dtree)            Call: rpart(formula = formula, data = inputData, method = "class",      command = rpart.control(minsplit = xxx, cp = 0.001))   north= 770              CP nsplit ane 0.496598639      0 2 0.013605442      1 3 0.008503401      vi 4 0.001000000     ten   rel error    xerror i 1.0000000 1.0000000 two 0.5034014 0.5170068 three 0.4353741 0.5646259 4 0.4013605 0.5442177         xstd ane 0.07418908 2 0.05630200 three 0.05854027 iv 0.05759793

Tree Pruning

The decision tree is and so "pruned", where inappropriate nodes are removed from the tree to preclude overfitting of the information:

#Clip the Tree and Plot pdtree<- prune(dtree, cp=dtree$cptable[which.min(dtree$cptable[,"xerror"]),"CP"]) plot(pdtree, uniform=TRUE,      main="Pruned Nomenclature Tree For Sales") text(pdtree, employ.n=TRUE, all=True, cex=.viii)

The model is now tested confronting the examination information, and we see that we accept a misclassification percentage of sixteen.75%. Clearly, the lower the better, since this indicates our model is more accurate at predicting the "real" data:

#Model Testing out   tabular array(out[1:193],testData$response) response_predicted   response_input   mean(response_input != response_predicted) # misclassification %            [one] 0.2844156

Solving Regression Problems With Determination Trees

When the dependent variable is numerical rather than categorical, we will want to prepare a regression tree instead as follows:

#Regression Tree fitreg <- rpart(CarSales~Age+Gender+Miles+Debt+Income,                 method="anova", data=inputData)  printcp(fitreg) plotcp(fitreg) summary(fitreg)  par(mfrow=c(1,two))  rsq.rpart(fitreg) # cross-validation results          


#Regression Tree fitreg   printcp(fitreg)            Regression tree: rpart(formula = CarSales ~ Age + Gender + Miles + Debt + Income,      data = inputData, method = "anova")  Variables actually used in tree structure: [1] Age    Debt   Income  Root node mistake: 6.283e+10/770 = 81597576  northward= 770           CP nsplit rel mistake 1 0.698021      0   1.00000 ii 0.094038      1   0.30198 iii 0.028161      2   0.20794 4 0.023332      4   0.15162 5 0.010000      v   0.12829    xerror     xstd i one.00162 0.033055 2 0.30373 0.016490 3 0.21261 0.012890 4 0.18149 0.013298 5 0.14781 0.013068          
plotcp(fitreg) summary(fitreg)            Call: rpart(formula = CarSales ~ Historic period + Gender + Miles + Debt + Income,      data = inputData, method = "anova")   n= 770             CP nsplit rel error 1 0.69802077      0 1.0000000 2 0.09403824      ane 0.3019792 3 0.02816107      2 0.2079410 iv 0.02333197      4 0.1516189 5 0.01000000      five 0.1282869      xerror       xstd 1 ane.0016159 0.03305536 2 0.3037301 0.01649002 iii 0.2126110 0.01289041 4 0.1814939 0.01329778 5 0.1478078 0.01306756  Variable importance   Debt  Miles Income    Age      53     23     20      4

Now, we prune our regression tree:

#Prune the Tree pfitreg<- clip(fitreg, cp=fitreg$cptable[which.min(fitreg$cptable[,"xerror"]),"CP"]) # from cptable    plot(pfitreg, uniform=TRUE,      master="Pruned Regression Tree for Sales") text(pfitreg, apply.n=True, all=TRUE, cex=.eight)

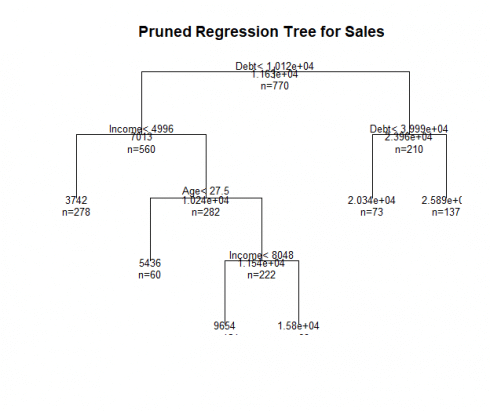
Random Forests

However, what if we have many decision trees that nosotros wish to fit without preventing overfitting? A solution to this is to use a random forest.

A random forest allows us to determine the most important predictors beyond the explanatory variables past generating many decision trees and then ranking the variables by importance.

library(randomForest) fitregforest   impress(fitregforest) # view results            Telephone call:  randomForest(formula = CarSales ~ Historic period + Gender + Miles + Debt +      Income, information = inputData)                 Type of random woods: regression                      Number of trees: 500 No. of variables tried at each split: 1            Hateful of squared residuals: 10341022                     % Var explained: 87.33 > importance(fitregforest) # importance of each predictor        IncNodePurity Age       5920357954 Gender     187391341 Miles    10811341575 Debt     21813952812 Income   12694331712

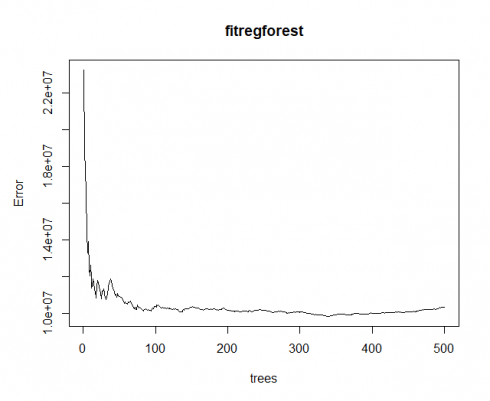
From the above, we see that debt is ranked equally the most important factor, i.e. customers with high debt levels will be more likely to spend a greater amount on a car. Nosotros see that 87.33% of the variation is "explained" past our random wood, and our error is minimized at roughly 100 trees.